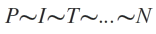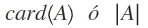Teselas de La Alhambra: Teselaciones Periódicas del Plano
Las calzadas romanas, tenían –entre otros- como objetivo el facilitar el paso de las personas, caravanas, animales, etc. Por tanto, una de las características más importantes que debieran cumplir sería que no admitiesen huecos para así evitar caídas y lesiones tanto de personas como de animales, generalmente cargados; es decir, se trataba de cubrir por completo la calzada; es, en este sentido, en el que podemos decir que una calzada romana es uno de los primeros ejemplos de la historia de la teselación, pues como veremos ahora una teselación, grosso modo, no es más que un recubrimiento del plano que no deja resquicios.
En la mitología griega las musas (en griego antiguo μοῦσαι mousai) eran, según los escritores más antiguos, las diosas inspiradoras de la música y, según las nociones posteriores, divinidades que presidían los diferentes tipos de poesía, así como las artes y las ciencias.
La palabra griega μoυσα-ης (mousa-es) significa ‘musa’; μουσειoς-α-oν (mouseios-a-on), ‘concerniente a las musas’; μoυσειoν-oυ (mouseion-ou), ‘templo de las musas’, ‘lugar donde residen las musas’.
Museo Arqueológico de Nîmes, Francia. Segunda mitad del siglo I a. C. La nadadora negra y el delfín.
La palabra μoυσειoν (mouseion) dio origen al latín musivus -a -um, que es el antecedente de mosaico. Se dice que los romanos consideraban tan exquisito el arte de hacer mosaicos que pensaban que solo podían crearlo las musas o los favorecidos por ellas.
Un mosaico (del latín mosaĭcum [opus], ‘[obra] relativa a las Musas, artística’) es una obra pictórica elaborada con pequeñas piezas de piedra, cerámica, vidrio u otros materiales similares de diversas formas y colores, llamadas teselas, unidas mediante yeso, u otro aglomerante, para formar composiciones decorativas geométricas o figurativas. Cuando las piezas empleadas son de madera se denomina taracea.
Suelo de la Domus Augustana
Teselas
La tesela es una pequeña pieza de piedra, terracota o vidrio coloreado que se utiliza para confeccionar un mosaico. La palabra proviene del latín tessella que, a su vez, procede del término griego τεσσερες.
Los romanos elaboraban los mosaicos con estas pequeñas piezas llamadas teselas, de ahí que se refiriesen a ellos también como opus o ars tessellatum. Las teselas son piezas de forma cúbica, hechas de rocas calcáreas o materiales de vidrio o cerámicas, muy cuidadas y elaboradas y de distintos tamaños. El artista las disponía sobre la superficie, como un rompecabezas, distribuyendo el color y la forma y aglomerándolas con una masa de conglomerante.
Parte de un mosaico romano del puerto de Ostia (Roma) del siglo II a.c.
En el mundo griego fue muy frecuente y desde muy temprano (desde fines del siglo V a. C.) el pavimento compuesto por guijas de río (piedrecillas que se encuentran en las orillas) de tamaños y de colores distintos. Con estas guijas se hacían dibujos sencillos de temas geométricos. A finales del siglo III a. C., las teselas vinieron a sustituir estos guijarros polícromos.
Los romanos llegaron a dominar el trabajo hecho con las teselas. Las primeras obras se hacían con teselas muy pequeñas y ya en época imperial el tamaño se hizo mayor, de un centímetro cuadrado. El mosaista llamado Sosos de Pérgamo hizo en el mosaico que se conoce con el nombre de Las palomas el trabajo de un gran profesional; este mosaico está compuesto con teselas muy pequeñas: sesenta teselas ocupan el espacio de un centímetro cuadrado.
Mosaico de Leda y el cisne en el Santuario de Afrodita (Palea Paphos), ahora en el Cyprus Museum, Nicosia.
Mosaico Villa Romana
Satiro y ninfa, mosaico romano, Casa del Fauno Pompeya.
Las teselas se colocaban sobre un lecho de conglomerante casi líquido. Era una técnica que puede compararse con el puntillismo de los pintores impresionistas del siglo XIX. Para fabricar un pavimento hecho de mosaico había que seguir una serie de pasos que con el tiempo se fueron perfeccionando. El lugar de fabricación era un taller especial. Allí lo primero que se hacía era diseñar el cuadro y este trabajo tomaba el nombre de emblema, voz tomada del griego que viene a significar «algo que se incrusta en».
Mosaico de las palomas, Museos Capitolinos.
Significado y Sinónimos
Tesela: Pieza de los dibujos de un mosaico.
El concepto de teselación no forma parte del diccionario de la Real Academia Española (RAE). El término que sí aparece es teselado, referido a aquello que se compone de teselas. Las teselas, a su vez, son los distintos fragmentos que forman parte de un mosaico (obra que se compone a partir de diferentes piezas o trozos).
Teselación: cubrir con teselas pavimentos, bóvedas,… cualquier superficie plana.
Sinónimos: Teselar, azulejar, alicatar, enlosar, embaldosar, solar, adoquinar, empedrar, pavimentar,…
Definición:
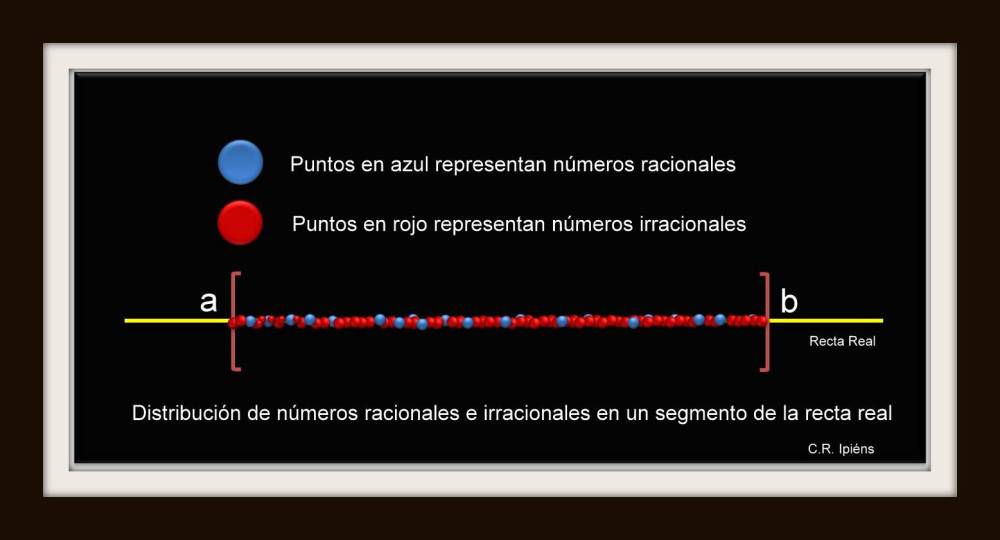
Una teselación (mosaico) del plano es una colección de regiones (Teselas, compactos con interior no vacío) llamadas “teselas” tales que:
- Dos teselas no tienen ningún punto interior en común, es decir, sólo pueden compartir parte de su frontera.
- La unión de las teselas cubre totalmente el plano.
Tipos de Teselaciones:
Un poco de Historia
En 1936 Alan Turing demostró la existencia de problemas o situaciones para los que no existen algoritmos finitos; entre estos problemas, que engrosaron los indecidibles de Gödel, se encuentran algunas cuestiones que plantean las teselaciones Aperiódicas o No Periódicas. Más recientemente se ha sumado a éstos “indecidibles”, el problema de si las ecuaciones diofánticas, -Sistemas de ecuaciones polinómicas de coeficientes enteros con soluciones enteras- poseen o no tales soluciones. En estos momentos no existe ningún argumento matemático fiable que avale tal cuestión.
Sin embargo, el ambiente geométrico en el que se desarrollan las teselaciones del plano y del espacio están gobernadas por este tipo de ecuaciones y gran número de ellas se encuentran determinadas de forma precisa.
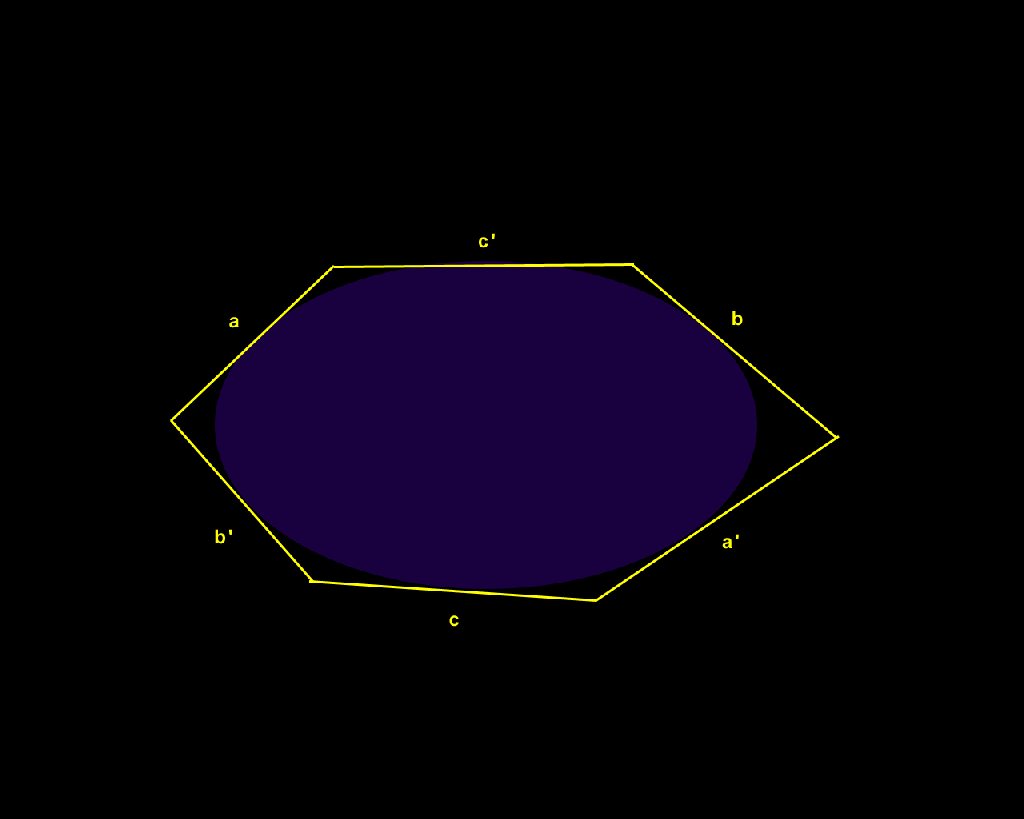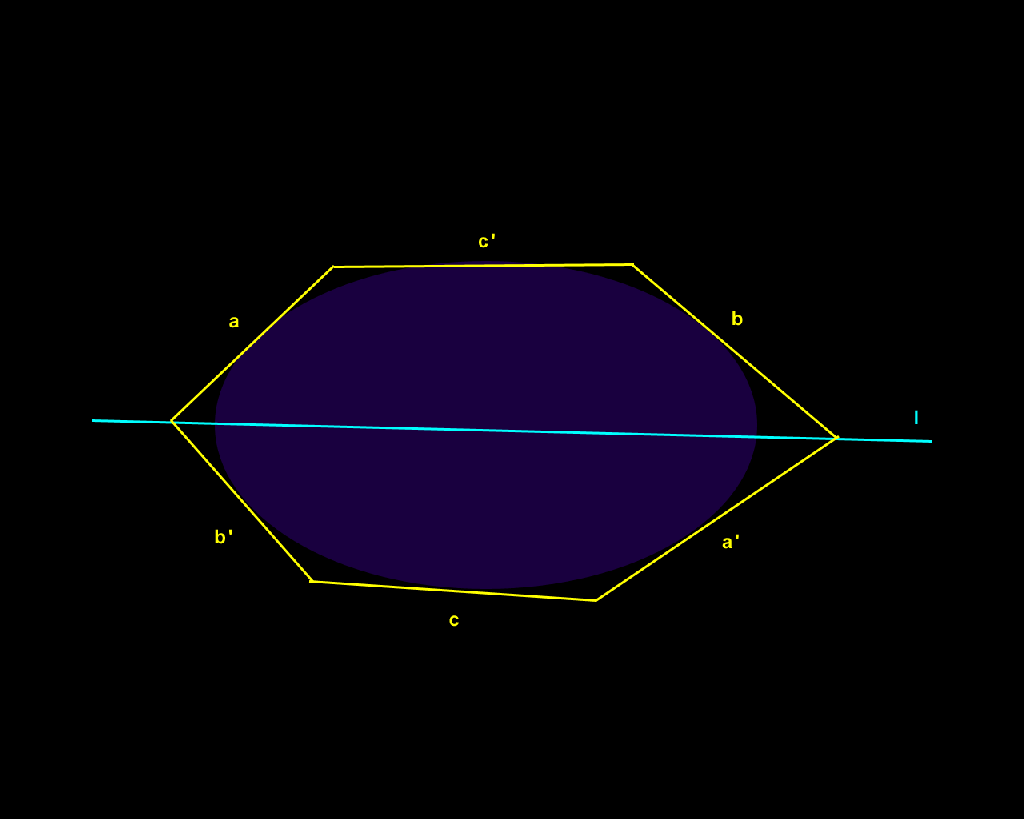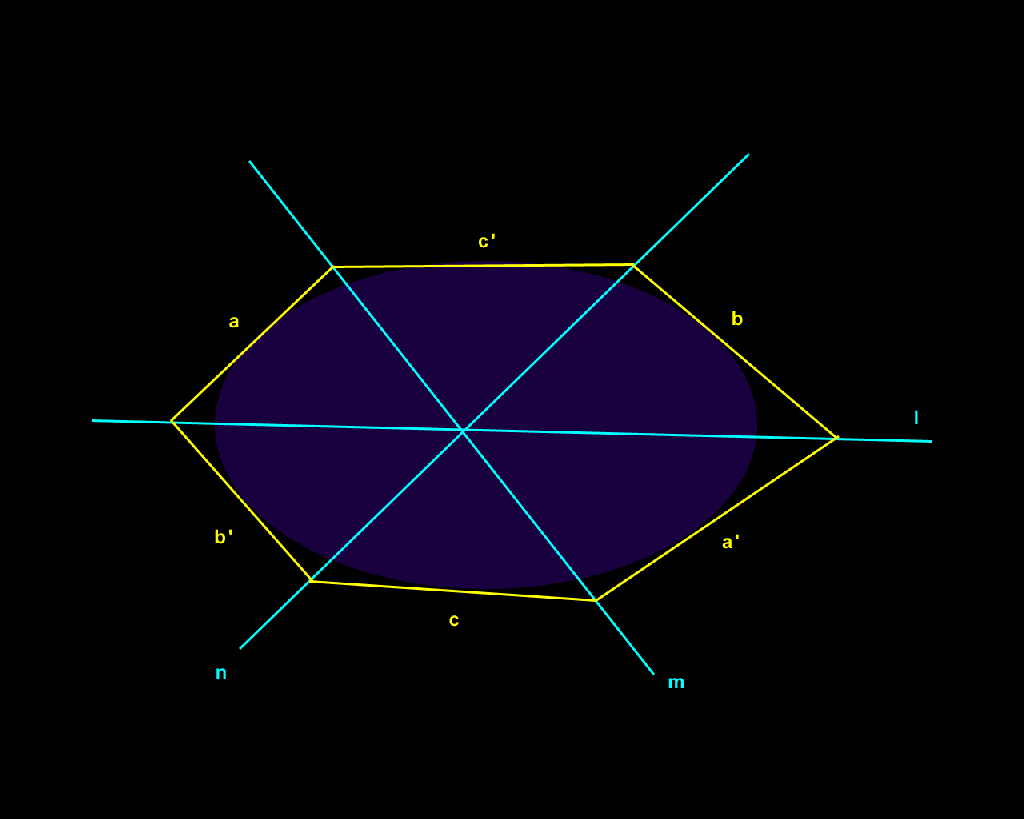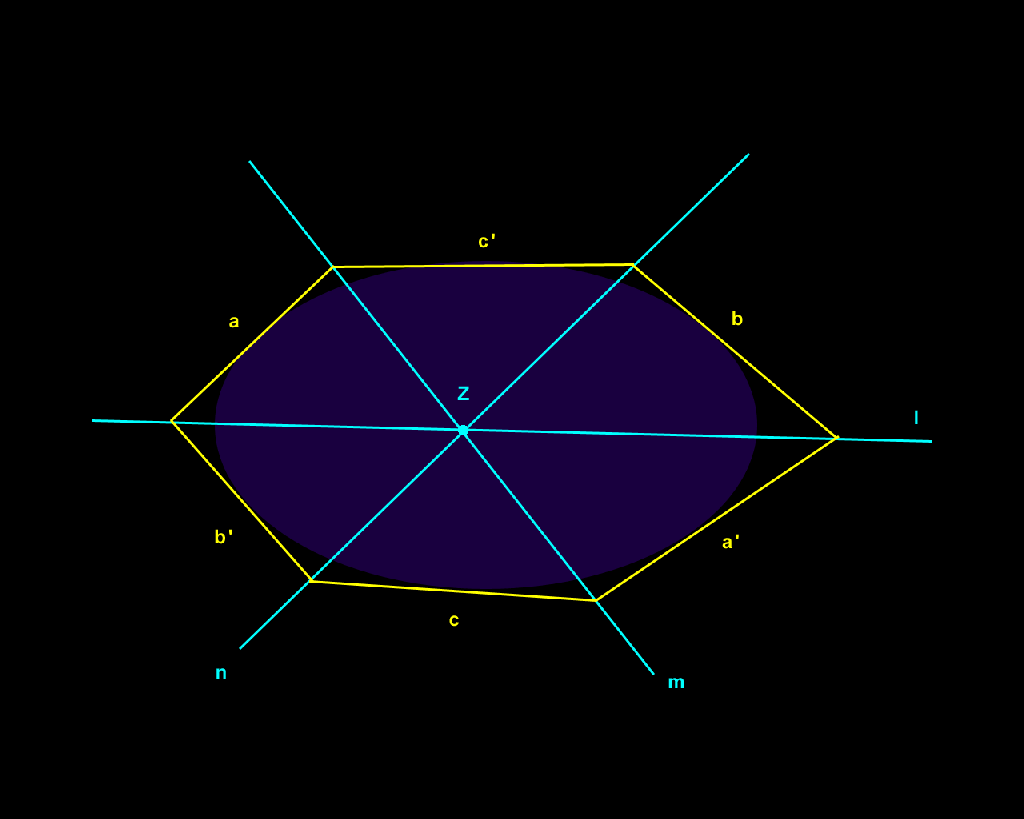
Una teselación se denomina “periódica” si existe una sección finita de la teselación (que puede estar formada por varias teselas) que permite mediante traslaciones en dos direcciones no paralelas (sin recurrir a giros o reflexiones), crear la teselación completa.
Una teselación es “aperiódica” o no periódica cuando no tiene traslaciones que hagan que coincida consigo misma.
Teselaciones periódicas: Teselaciones poligonales
Si nos planteamos un método eficaz con el que poder construir mosaicos fácilmente nos encontraremos con que un modo sencillo de hacerlo es usando distintos polígonos. No tenemos más que pensar en las típicas baldosas que ocupan los espacios de nuestras cocinas o los suelos. Si el mosaico está formado por un único tipo de polígonos regulares iguales se dice que el mosaico o la teselación es regular y, si está formado por más de un tipo de polígono regular se dice que es semi-regular. Si los polígonos son irregulares, decimos que la teselación es irregular.
Teselaciones Regulares.
Un primer planteamiento en el estudio de cómo teselar periódicamente el plano, sería el de la utilización de teselas poligonales. Diseños con este tipo de teselas aparecen en motivos ornamentales de múltiples culturas (egipcia, griega, china, árabe…). Los mosaicos poligonales planos han sido detalladamente estudiados.
El primer paso, consiste en emplear un único polígono regular.
Encontrar los polígonos regulares que teselan el plano, se reduce a resolver la siguiente ecuación diofántica:
Siendo x1 el número de polígonos y x2 el número de lados que concurren en un vértice. Las soluciones que se obtienen para esta ecuación son:
X1=6; x2=3, es decir, seis triángulos.
Nota: Para teselar el plano será necesario que los ángulos que concurran en un vértice sumen 360º. (Entendemos 360º por Plano)
Una segunda solución es: X1=4; x2=4, es decir, cuatro cuadrados. Para que un cuadrado tesele el plano será necesario que concurran 4 figuras en un mismo vértice, pues: 360º : 90º = 4
Por último, una tercera solución es la que viene dada por: X1=3; x2=6, es decir, tres hexágonos.
Como en las figuras anteriores podemos deducir que necesitamos que concurran 3 hexágonos en un vértice para teselar el plano, ya que: 360º/120º=3
Paseo de Gracia (Gaudí)
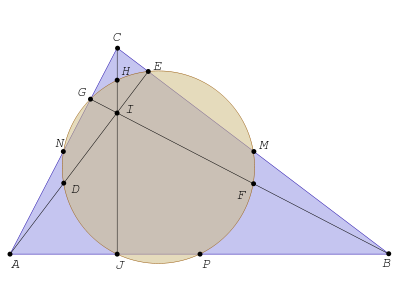
Vemos que el plano no se puede recubrir con pentágonos regulares puesto que 360º no es divisible por 108º que es la medida de un ángulo interior de un pentágono: 360º = 3 · 108º + 36º.
En general, tal como se ha mencionado anteriormente, para poder teselar el plano será necesario que los ángulos que concurran en un vértice sumen 360º (identificamos el plano con 360º) para que no queden huecos y poder ocupar todo el espacio del mosaico.
El siguiente paso sería plantear teselaciones con más de un polígono regular, a este nuevo tipo de teselaciones les llamamos semi-regulares.
Teselaciones Semi-regulares
Una Teselación semi-regular consiste en una pavimentación del plano con un mosaico d polígonos regulares de vértices comunes y arbitrario número de lados; conocer el número posible de ellas, se reduce a resolver la ecuación:
Donde mi es el número de polígonos de xi lados que concurren en un vértice.
Para el caso de sólo dos tipos de polígonos, la ecuación anterior adquiere la forma:
Que posee el siguiente conjunto de soluciones (Seis):
- m1=3, m2=2; x1=3, x2=4: Tres triángulos y dos cuadrados.
- m1=2, m2=2; x1=3, x2=6: Dos triángulos y dos hexágonos.
- m1=4, m2=1; x1=3, x2=6: Cuatro triángulos y un hexágono.
- m1=1, m2=2; x1=3, x2=12: Un triángulo y Dos dodecágonos.
- m1=1, m2=2; x1=4, x2=8; Un cuadrado y dos octógonos.
- m1=2, m2=1; x1=5, x2=10; Dos pentágonos y un decágono.
Para el caso de tres polígonos se incorporan dos soluciones más:
- Un triángulo dos cuadrados y un Hexágono
- Un cuadrado, un hexágono y un dodecágono:
Teselaciones Demi-Regulares
Una teselación demi-regular, también llamada una teselación polimorfa, es un tipo de teselación cuya definición es un tanto problemática. Algunos autores las definen como composiciones ordenadas de las tres regulares y las ocho teselaciones semirregulares, mientras que otros los definen como un mosaico que tiene más de una clase transitividad de vértices (que conduce a un número infinito de posibles teselados).
El número de mosaicos demi-regular comúnmente se da como 14 (Critchlow 1970; Ghyka 1977; Williams 1979; Steinhaus 1999). Sin embargo, no todas las fuentes aparentemente dan el mismo resultado. Por lo tanto, es necesario tener precaución al tratar de determinar qué se entiende por «teselación demi-regular.»
Los 20 teselados de la ilustración anterior fueron descubiertos por primera vez, por Krötenheerdt en 1969; Grünbaum y Shephard en 1986 estructurarían estos teselados con más precisión.
Cuando sólo usamos los tres teselados regulares y los 8 teselados semi-regulares. Existen 14 teselados demi-regulares. Algunos de ellos son:
Teselaciones Irregulares
Hay múltiples métodos para construir teselaciones poligonales con formas irregulares. Uno de ellos consiste en modificar polígonos que teselen el plano de forma que los polígonos resultantes permitan el “encaje” con otra tesela con igual forma.
Los teselados irregulares están construidos a partir de polígonos regulares e irregulares que al igual que todas las teselaciones cubren toda la superficie sin sobreponerse y sin dejar espacios vacíos. La distribución de los polígonos en los distintos vértices es cíclica, pueden darse 3, 4, 5 y más distribuciones que harán que la periodicidad sea más espaciada requiriendo dibujar una gran porción de la tesela para poder ver un ciclo completo, para tal efecto veamos dos ejemplos de la distribución del pentágono:
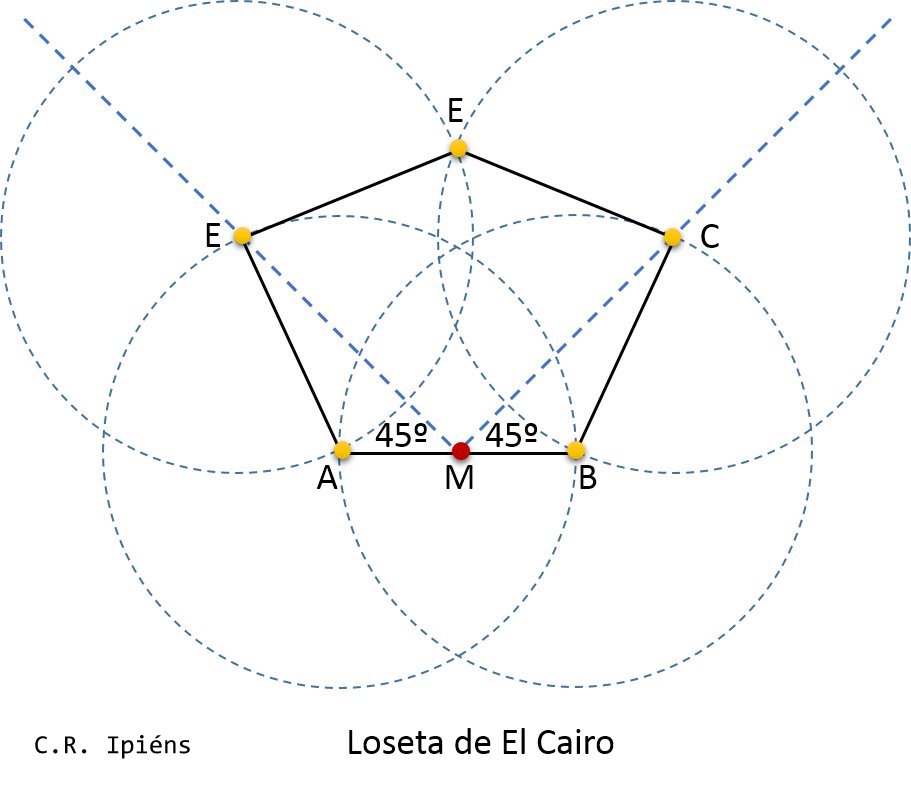
Teselación de El Cairo
Hay algunos polígonos especiales que dan lugar a mosaicos muy vistosos como el Mosaico del Cairo, que recibe su nombre por estar presente con frecuencia en los pavimentos de esa ciudad egipcia y en los murales y arte islámico, de ahí su nombre.
El pentágono posee aquí 5 lados de la misma medida. Tiene dos ángulos rectos, un ángulo de 144° y dos ángulos de 108°.Como para todo pentágono, la suma de sus ángulos es de 540°
Ver clip
La Teselación pentagonal de El Cairo, puede considerarse también hexagonal.
Pavimento en El Cairo
Los teselados de la Alhambra y Escher
Mosaicos en la Alhambra con el símbolo de Carlos V.
Un azulejo renacentista, con una corona, la pavimentación en el suelo en la Alhambra de Granada, España.
Siempre había sido un enigma saber cuántas formas había para rellenar el plano con las teselas al estilo de la Alhambra. Se conocía como el problema del teselado o del friso. Había conjeturas pero no fue hasta 1910 que Ludwig Bieberbach primero demostró que el número de formas de solucionarlo era finito y posteriormente que solo había diecisiete formas simples de hacerlo.
Lacerías en la Alhambra
Existen en la naturaleza diecisiete grupos cristalográficos planos, que se corresponde con el problema de las teselas. Pero un tema curioso es que hasta hace muy poco tan solo se habían identificado trece de ellos. Recientemente han aparecido los cuatro que faltaban.
En los adornos ornamentales de suelos y paredes de la Alhambra se pueden encontrar ejemplos de cada uno de los grupos cristalográficos planos. Quizás no resulta sorprendente que en la Naturaleza aparezcan los 17 grupos, pero desde luego lo es que en la Alhambra de Granada puedan verse materializados en sus adornos. Los creadores de los mosaicos de la Alhambra de Granada no podían conocer el teorema de clasificación de Fedorov, y por lo tanto no conocían cuántos grupos de simetrías podían usarse para rellenar el plano con baldosas(teselación del plano), por eso resulta impactante que conocieran todos y cada uno de los 17 existentes.
El arte desarrollado por los árabes en la península Ibérica, presenta un gran desarrollo del concepto de simetría, debido a su carácter abstracto. De acuerdo a los principios religiosos les estaba estrictamente prohibido a los artistas musulmanes representar seres vivientes en sus creaciones. Esta limitación, en lugar de empobrecer su creatividad, sirvió de aliciente para estimular sus mentes y lanzarse por caminos de gran belleza y originalidad. Su conocimiento de las simetrías alcanzó tal grado de magnitud que fueron los únicos en descubrir y utilizar sabiamente en sus decoraciones los 17 tipos de simetría plana.
Este motivo hace que la Alhambra de Granada tenga ese especial interés para los matemáticos, ya que los artistas andalusíes-granadinos pusieron de manifiesto con su trabajo una nueva forma de abordar el trabajo científico buscando nuevas ideas desde el ejercicio libre y audaz del método creativo, basado en hacer variaciones sobre una misma figura.
La Alhambra es, actualmente, el único monumento construido antes del descubrimiento de la teoría de grupos que cuenta con al menos un ejemplo de cada uno de los grupos cristalográficos planos.
Apuntes originales de Escher, La Alhambra 1936.
Después de visitar la Alhambra por primera vez, Escher intentó unos nuevos diseños, de los que se conservan bocetos de 1926, todavía muy rudimentarios. Tras una segunda visita, esta vez junto con su mujer, en 1936, copió durante varios días motivos allí representados y descubrió un sistema para representar particiones periódicas del plano, consiguiendo descubrir los 17 grupos de simetría planos que figuran en la Alhambra, a pesar de sus rudimentarios conocimientos matemáticos. Pero no se detuvo aquí, sino que además introdujo el color, cosa que nadie había hecho hasta esa fecha.
Las cinco Teselas que más se repiten en los mosaicos de La Alhambra se llaman “el hueso”, “el pez volador”, ”el avión” , “la pajarita”, “el pétalo” y aunque no es propiamente una tesela “el sello de Salomón” es de las ornamentaciones más frecuentes.
Sello de Salomón
El Avión (Construcción)
El Avión o El Sombrero (Construcción)
El pétalo (Construcción)
El Hueso (Construcción)
Escher en relieve
ver clip
Todo lo relatado en este artículo se refiere a teselaciones periódicas del plano. En una próxima entrada sobre teselaciones, completaremos el tema tratando las Teselaciones NO periódicas. Queda pendiente.
Variaciones (2)
. El contenido principal de Plimpton 322 es una tabla de números, con cuatro columnas y quince filas, en notación sexagesimal babilónica. Otto E. Neugebauer (1957) aboga por una interpretación de Teoría de Números, señalando que esta tableta provee una lista de (pares de números que conforman) ternas pitagóricas. Por ejemplo, la línea 11 de la tabla se puede interpretar como la descripción de un triángulo con el lado corto de 3/4 y la hipotenusa 5/4, que forma el lado: relación hipotenusa de la familiar (3,4,5) del triángulo rectángulo. Si p y q son dos números primos entonces 
forma una triple pitagórico, y todos los triples pitagóricos se pueden formar de esta manera o como múltiplos de una triple formó de esta manera.
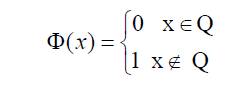
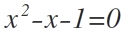
![Biyección entre [0,1] y R](http://euclides59.files.wordpress.com/2013/01/daum_equation_1357910889781.png)
Cosmos y Matemáticas 